Recent articles have focused much effort on studying the stochastic behavior of secondary electron exposure of EUV resists [1-4]. Here, we consider the implications of extending similar treatments to DUV lithography.
Basic Model Setup
As before, the model uses pixel-by-pixel calculations of absorbed photon dose, followed by a quantum yield of acids (previously secondary electrons for EUV [1-2]) per pixel, with both absorbed photon number and acid generation values being subject to Poisson statistics. Gaussian blur is then applied per pixel; however, unlike conventional considerations, the blur scale parameter (often known as sigma) is itself another number randomly chosen from a range or distribution. Smoothing can be finally applied to give more visually realistic images.
Acid Diffusion Length
Experimentally, it was found that secondary electron blur increased with dose and would itself follow an exponential or normal distribution [1-2,5]. Likewise, acid diffusion lengths should also be considered to follow a similar distribution. From the literature, we note that (1) it is not dependent on dose [6], and (2) it is in fact obviously dependent on bake temperature and time [7-8]. Generally, the diffusion length is given as 2*sqrt(Dt), where D is the diffusion coefficient, and t is the time elapsed (during bake). So, the range or distribution of acid diffusion lengths corresponds to that of the diffusion coefficient. From the values in the references [6,8], we can estimate a standard deviation of ~1 nm. The target value of the acid diffusion length should, of course, be sufficiently smaller than the target critical dimension (CD), e.g., 40 nm.
ArF Immersion Example (80 nm pitch)
Following [6], we may take a target diffusion length value of 10 nm with +/-7 standard deviations of +/-7nm, giving a range of 3-17 nm. The absorbed dose is taken to be 10% of the nominal dose of 30 mJ/cm2. The acid quantum yield is assumed to be 0.33. The worst case would be at +7 standard deviations, or 17nm, with a probability of 1.28e-12. We examine the typical and worst cases below.
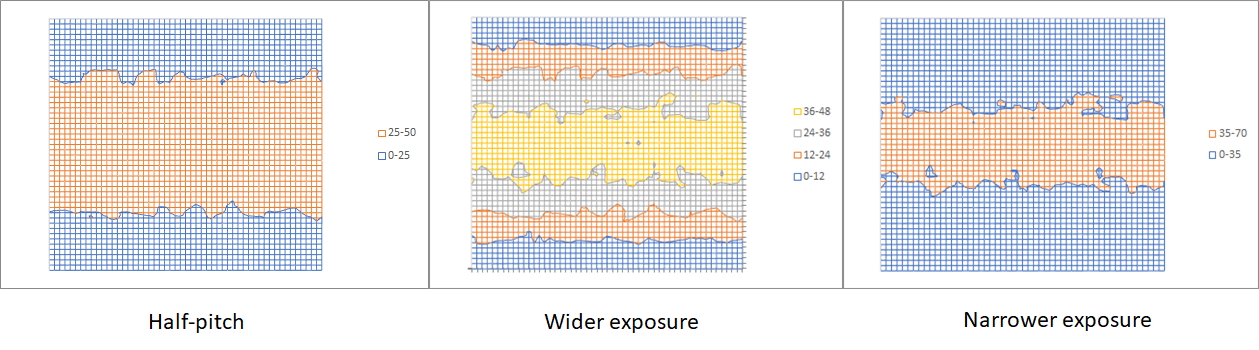
Figure 1. Typical acid deprotected image for 10nm acid diffusion length. 3 mJ/cm2 absorbed over 80 nm line pitch. Left: half-pitch target. Center: wider exposed feature target. Right: narrower exposed feature target.
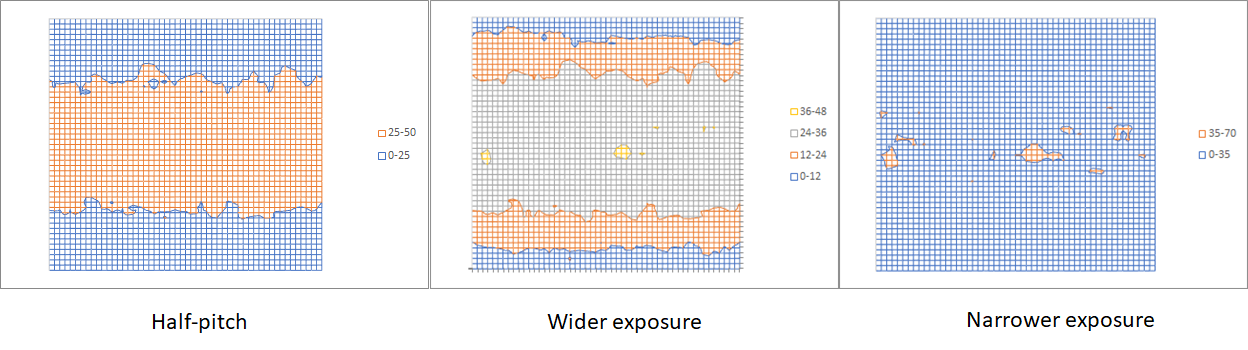
Figure 2. +7 standard deviation deprotected image with 17 nm acid diffusion length. 3 mJ/cm2 absorbed over 80 nm pitch. Left: half-pitch target. Center: wider exposed feature target. Right: narrower exposed feature target.
The trend seems to be that narrower exposed feature are most sensitive to stochastic defects, and edge roughness would be most commonly observed. Obvious means to address these issues would be higher doses and more absorptive resists. Increasing the absorbed dose to 8 mJ/cm2 (e.g., 20% absorbed from 40 mJ/cm2) gives us the following.
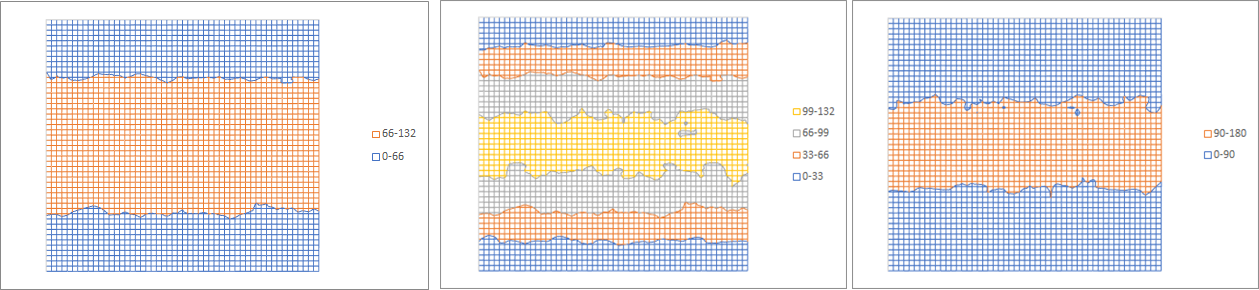
Figure 3. Typical acid deprotected image for 10nm acid diffusion length. 8 mJ/cm2 absorbed over 80 nm line pitch. Left: half-pitch target. Center: wider exposed feature target. Right: narrower exposed feature target.
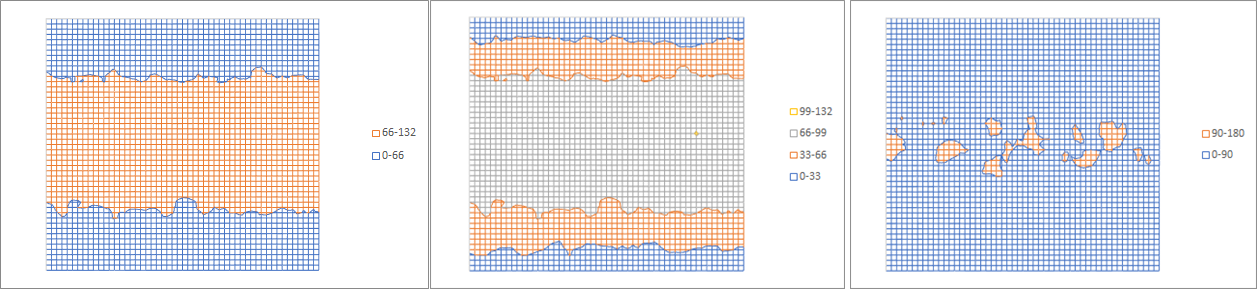
Figure 4. +7 standard deviation deprotected image with 17 nm acid diffusion length. 8 mJ/cm2 absorbed over 80 nm pitch. Left: half-pitch target. Center: wider exposed feature target. Right: narrower exposed feature target.
Clearly, the higher dose helps to smoothe out the roughness, but the narrow exposed feature is still vulnerable to becoming defective at a low rate. With brightfield attenuated phase-shift masks becoming a standard for improving NILS [9], narrow exposed features can be practically avoided anyway.
References
[1] F. Chen, Modeling EUV Stochastic Defects with Secondary Electron Blur, https://www.linkedin.com/pulse/modeling-euv-stochastic-defects-secondary-electron-blur-chen
[2] F. Chen, Secondary Electron Blur as the Origin of EUV Stochastic Defects, https://www.linkedin.com/pulse/secondary-electron-blur-randomness-origin-euv-stochastic-chen
[3] H. Fukuda, Localized and cascading secondary electron generation as causes of stochastic defects in extreme ultraviolet projection lithography, J. Microlith./Nanolith. MEMS MOEMS 18, 013503 (2019), https://www.spiedigitallibrary.org/journals/journal-of-micro-nanolithography-mems-and-moems/volume-18/issue-1/013503/Localized-and-cascading-secondary-electron-generation-as-causes-of-stochastic/10.1117/1.JMM.18.1.013503.full
[4] H. Fukuda, Cascade and cluster of correlated reactions as causes of stochastic defects in extreme ultraviolet lithography, J. Microlith./Nanolith. MEMS MOEMS 19, 024601 (2020), https://www.spiedigitallibrary.org/journals/journal-of-micro-nanolithography-mems-and-moems/volume-19/issue-2/024601/Cascade-and-cluster-of-correlated-reactions-as-causes-of-stochastic/10.1117/1.JMM.19.2.024601.full
[5] F. Chen, EUV Stochastic Defects from Secondary Electron Blur Increasing With Dose, https://www.youtube.com/watch?v=Q169SHHRvXE
[6] M. Yoshii et al., Influence of resist blur on resolution of hyper-NA immersion lithography beyond 45-nm half-pitch, J. Microlith./Nanolith. MEMS MOEMS 8, 013003 (2009).
[7] D. Van Steenwinckel et al., Lithographic importance of acid diffusion in chemically amplified resists, Proc. SPIE 5753, 269 (2005).
[8] M. D. Stewart et al., Acid catalyst mobility in resist resins, JVST B 20, 2946 (2002).
[9] F. Chen, “Phase-Shifting Masks for NILS Improvement – A Handicap for EUV?”, https://www.linkedin.com/pulse/phase-shifting-masks-nils-improvement-handicap-euv-frederick-chen
Also Read:
Advancing Semiconductor Processes with Novel Extreme UV Photoresist Materials
Modeling EUV Stochastic Defects with Secondary Electron Blur
Enhanced Stochastic Imaging in High-NA EUV Lithography
Share this post via:





Has ASML Reached the Great Wall of China