Formal Datapath Verification for ML Accelerators

Formal methods for digital verification have advanced enormously over the last couple of decades, mostly in support of verification in control and data transport logic. The popular view had been that datapath logic was not amenable to such techniques. Control/transport proofs depend on property verification; if a proof is found in a limited state space it is established absolutely. For large designs the check is often “bounded” – proven correct out to some number of cycles but not beyond. Experienced product teams generally had no problem with this limitation. Most electronic products allow for some threshold – perhaps 2 weeks or a month – before a reset is needed. But for one class of functions, datapaths, we will not tolerate any errors. These require a completely different approach to formal verification, which proves to be very important for math-intensive ML accelerators.

What are datapaths and why are they hard to verify?

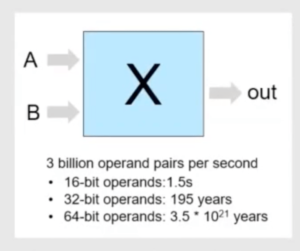
A datapath is the part of a compute engine that does data processing, particularly math processing. It typically supports integers, fixed point numbers and floating-point numbers, with a range of precision options. Operations span from basic arithmetic to exponents and logs, trig, hyperbolic trig and more. Our intolerance of even occasional errors in such functionality was most infamously demonstrated by the Pentium FPDIV bug, estimated to occur in only one in 9 billion operations yet considered responsible for a $475M charge for replacement and write-off and a significant black eye for Intel. (In fairness, Intel are now leaders in applying and advancing state-of-the-art formal methods for more complete proving.)

Datapath verification (DPV) far exceeds the reach of simulation, as illustrated in the figure above. Faster machines and massive parallelism barely dent these numbers. Formal methods should shine in such cases. But property checking quickly runs out of gas because bounded model checkers (like SAT) can only search out through so many cycles before an exponentially expanding design state space becomes unmanageable. Instead, formal methods for datapaths are based on equivalence checking. Here equivalence is tested not between RTL and gate-level designs, but between RTL and reference C (or C++ or SystemC) models. If the reference model is widely trusted (such as Soft-float) this comparison should provide high confidence in the quality of the implementation.

VC Formal DPV and the Synopsys ARC NPX6 NPU Processor for AI

Synopsys recently hosted a webinar on application of their formal datapath verifier built on these principles. After an intro to the tool from Neelabja Dutta, Shuaiyu Jiang of the ARC group described how he used VC Formal DPV to verify datapath logic for their ARC NP6X Neural Processing Unit (NPU) IP.

The convolution accelerator example is useful to understand how the ARC team decomposed the verification task for what I think of as an assume/verify strategy though here applied to equivalence checking. The multiply phase is one such sub-component. Here assumptions would be that inputs to the C reference and the RTL implementation must be the same. In place of an output property check the proof defines a “lemma” requiring the outputs are the same. A similar process is run over each component in the convolution accelerator, followed by a top-level check for the assembled sub-proofs.

Shuaiyu also talks about application to the ARC Generic Tensor Ops Accelerator (GTOA). Briefly, ML frameworks (TensorFlow, TF-Lite, PyTorch, JAX, etc) work with tensor objects – here 2D image x color depth x sample size for a 4D tensor. These build on large sets of operators somewhat unique to each network (>1000 for TF), impeding portability, uniformity, etc. Following the ISA philosophy, Arm developed and open-released TOSA – Tensor Operator Set Architecture with ~70 basic instructions. TOSA-compliant frameworks and inference platforms should eliminate such inconsistencies. Though Shuaiyu did not comment on this point I assume ARC GTOA is built in line with the TOSA approach. The ARC ALU for these operations is necessarily even more math intensive than the convolution example, making it an even better example for DPV proofs, suitably decomposed.

To learn more

You can register to watch the webinar HERE. Also I suggest you read the second edition of “Finding Your Way Through Formal Verification (Second Edition)”. This has been updated in several areas since Synopsys released the first edition five years ago. There is a whole chapter now dedicated to DPV. Well worth a read – I’m a co-author 😀