In an earlier article [1], the resolution limit for the space between paired features was described by the Rayleigh criterion of ~0.6 wavelength/numerical aperture, where the numerical aperture (NA) represented the sine of the largest angle for a ray focused from the lens to a point. It is also given by the radius of the lens divided by the focusing distance (or focal length). Yet, it is quite common practice in semiconductor device lithography to work with images with sizes of, say, ~0.4 wavelength/NA. While it is still possible to have images below the Rayleigh criterion, they will face some fundamental difficulties.
The Rayleigh unit of defocus
For the upcoming discussion, it is important to have a reference scale for defocus. The Rayleigh unit (RU) of defocus (0.5 wavelength/(NA)^2) has been used by many authors [2-6]. The proof is given in [6] and is derived from the optical path difference between a ray traveling along the optical axis and a ray from the edge of the lens (pupil) to the point of focus.
The canary: an isolated feature (line) pair
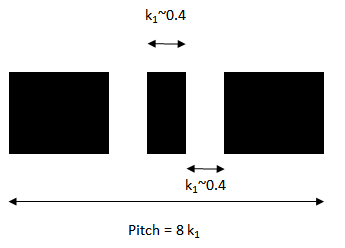
As a reference we will consider a pair of lines targeted at a width of 0.4 wavelength/NA and separated by the same distance (Figure 1). This pair of lines is repeated as well, at a pitch of 8x the linewidth, i.e., 3.2 wavelength/NA. Also, for simplicity, the object to be imaged is actually an opaque film with only two openings corresponding to the lines. In leading-edge lithography systems, the object is four time (4x) the size of the targeted image on the wafer.
Figure 1. Pair of lines (k1 ~ 0.4), separated by gap of same width (plan view). The pair of line is repeated on a pitch 8x the linewidth.
On-axis illumination
First, we look at the on-axis illumination case, which is simplest. It is also some times referred to as sigma=0, where sigma is the ratio of illumination radius in the pupil to the NA. Under this condition, we find that defocus has a noticeable effect on the observed “pitch”, i.e., the center-to-center distance between the two lines (Figure 2).
Figure 2. Defocus narrows the observed pitch between the two lines, under on-axis illumination. The dotted line indicates the threshold intensity at which the image is printed. Under defocus, both edges of the lines are shifted inward.
The underlying reason comes from the diffraction analysis. Under on-axis illumination, the pattern is formed from the interference of seven diffraction orders (labeled -3, -2, -1, 0, 1, 2, 3), separated in spatial frequency at an interval of wavelength/pitch. The normalized electric field amplitudes of the diffraction orders are shown as a spectrum in Figure 3. When defocused, the diffraction orders propagating closest to the NA (-3 and 3) deviate most in optical path from the axis. They determine the positions of the peaks and the trough in between, leading to the narrowed gap.
Figure 3. Normalized electric field amplitudes for the diffraction orders with and without defocus.
At one full Rayleigh unit of defocus, the lines are essentially merged:
Figure 4. The pair of lines are merged at 1 Rayleigh unit of defocus.
Pitch has no practical meaning here as it is completely determined by the focusing of the gap between the lines, which in turn is affected by the true pitch of 8x the linewidth, i.e., 3.2 wavelength/NA.
Slightly off-axis illumination (sigma=0.3, parallel to lines), with truncation of diffraction spectrum
Next, we consider illumination that is slightly off-axis in the direction parallel to the lines. It is about a third of the pupil radius offset from the center. Consequently, the -3 and +3 orders considered significant in the on-axis case are now truncated. The next highest orders, -2 and +2 were not that significant to begin with, so the image is determined mainly by the 0th, -1st and +1st orders. This only allows one peak per pitch (Figure 5).
Figure 5. With slightly off-axis (parallel to the lines) illumination, the highest diffraction orders from the on-axis case are truncated. This leaves the image mainly determined by orders -1, 0, and 1. Only a single peak may be achieved per pitch.
The truncated diffraction order spectrum also looks very similar even under defocus (Figure 6).
Figure 6. With the truncation of the -3rd and +3rd orders, the diffraction order spectrum is now hardly impacted by defocus.
The truncation of the -3rd and +3rd essentially obliterated the target pattern, despite giving much better defocus tolerance. Truncation of the diffraction spectrum also explains enlarged tip-to-tip distance when dipole illumination is used for minimum pitch lines [7], with no help available from optical proximity correction (OPC) [8].
Do Sub-Resolution Assist Features help?
As mentioned in the previous article [1], arrayed features offer a way to go below the Rayleigh criterion. One possibility is to pretend to print an entire array but use subresolution width (or subresolution assist features (SRAFs)) to not print the parts other than the selected locations (Figure 7) [9]. The illumination is also adjusted to match the ideal dipole point locations for the pitch corresponding to the line pair.
Figure 7. Sub-resolution assist features are an imperfect simulation of an extended array, by means of adding extra features (the outer lines here, plan view) which are too small to print.
The impact on the diffraction order spectrum is shown in Figure 8.
Figure 8. Diffraction order spectrum after SRAFs are applied.
The 0th and 4th orders correspond to the 0th and 1st orders of the pitch corresponding to the line pair. This helps reinforce the distance between the lines. However, it also becomes possible to print unwanted lines at the same pitch if the dose is too high. This can be avoided by having the subresolution assist width sufficiently small compared to the main line width. This is the role of the other diffraction orders. However, with the other orders remaining significant, the defocus affects linewidth quite significantly. Moreover, there is still some pitch walking due to defocus (Figure 9).
Figure 9. Defocus causes some pitch walking even when SRAFs are used, pushing the lines slightly further apart.
The defocus causes the lines to shift away from each other, unlike the on-axis illumination case without SRAFs. The +1st order is the dominant influence here. At just a little over 1 Rayleigh unit of defocus, the lines disappear (Figure 10).
Figure 10. At a little over 1 Rayleigh unit of defocus, the line pair disappears, despite the use of SRAFs.
Thus, the SRAF approach does not offer much improvement of the defocus tolerance.
By continuing to increase the defocus, to double this value, we see more clearly the extent of continued pitch walking through defocus:
Figure 11. At 2.1 Rayleigh units of defocus, the extent of pitch walking even when using SRAFs is very clear.
The assist feature is essentially a “blur” on the outside of the pair of lines. As the lines are defocused, they more easily merge with the “blur” than each other, thus moving them outward instead of inward.
How to print the target feature while preserving pitch through defocus?
It is now clear that the target feature as drawn in Figure 1 cannot be printed directly without issues of pitch preservation through defocus and the above approaches cannot even preserve the image up to 1 Rayleigh unit of defocus. Other approaches described in [1] may be applied: (1) double patterning or (2) patterning an array (in the true sense, not with SRAFs) and then trimming to keep only the pair in question. The second option has better overlay tolerance with self-aligned patterning, e.g., see [10].
Conclusion
Pitch is not practically fixed for an isolated pair of features as it is vulnerable to defocus. Some non-optimal illuminations completely wipe out any appearance of pitch. It can only be appropriate to apply pitch to describe truly arrayed features.
Appendix: Rayleigh unit of defocus
In this section, we present the proof of the derivation of the Rayleigh unit of defocus, from [6]. The idea is to calculate the optical path difference between a ray from the lens center traveling down the axis and a ray from the edge of the lens to the focal point. The distance along the axis over which the path difference ranges from zero to a quarter wavelength gives the depth of focus. Basically, two waves which are 90 degrees out of phase (corresponding to a quarter wavelength difference) would not interfere with each other but effectively add in quadrature as if incoherent. The path difference for an axial distance D and angle theta between the two rays is given by D(1-cos(theta)) ~ D * 2* (sin(theta/2))^2. Estimating sin(theta/2)~NA/2 gives D * 2 * (NA/2)^2 equal to the quarter wavelength, which in turn gives D = (1/2) wavelength/(NA)^2.
References
[1] https://www.linkedin.com/pulse/lithography-resolution-limits-paired-features-frederick-chen/
[2] https://www.jstage.jst.go.jp/article/photopolymer1988/2/3/2_3_375/_pdf
[3] H. J. Levinson, Principle of Lithography, SPIE Press, 2005, p. 35.
[4] https://patents.google.com/patent/US6327033
[5] W. B. Glendinning and J. N. Helbert (ed.), Handbook of VLSI Microlithography: Principles, Technology and Applications, Noyes Publications, 1991, p. 273
[6] L. F. Thompson, C. Grant Willson, and M. J. Bowden, Introduction to Microlithography, ACS, 1994, p. 76.
[7] M. Eurlings et al., Proc. SPIE 4404, 266 (2001).
[8] T. Matsuda wt al., Proc. SPIE 7973, 797316 (2011).
[9] https://vlsicad.ucsd.edu/Publications/Conferences/186/c186.pdf
[10] https://www.cerc.utexas.edu/utda/publications/C117.pdf
Share this post via:















TSMC N3 Process Technology Wiki