Stochastic Effects Blur the Resolution Limit of EUV Lithography

Conventionally, the resolution limit of a lithography system with wavelength l and numerical aperture NA is given by half-pitch = 0.25 wavelength/NA. With the use of EUV lithography, however, electron blur needs to be added [1]. The impact of this blur is to reduce the contrast [2]. Blur reduces the modulation amplitude by a factor of exp(-0.5*(2*pi*blur/pitch)²). Consequently, the normalized image log-slope (NILS) can drop below the target value of 2.0 (10% CD change for 10% dose change).

Another, more serious issue with EUV lithography, has been its stochastic behavior. Ideally, even with blur, we expect a straight-line image to be projected from a straight line on the mask, with smooth edges. In reality, we expect varying blur from electron scattering due to resist homogeneity. Besides locally varying blur, the number of absorbed photons per square nm varies according to Poisson statistics (std. dev. = sqrt(mean)). We also expect locally varying electron yield per absorbed EUV photon [3-6]. Thus, the actual image formed will have randomness, or stochasticity.

Figure 1. Scattered electron density plotted for 30 nm, 40 nm, and 50 nm pitch horizontal lines. Absorbed dose=60 mJ/cm², resist thickness = pitch, 5/um absorption, 3-5 electrons/absorbed photon, mean blur = 5 nm, blur std. dev. = 1 nm. The pixel size is 1 nm.

The smaller the pitch, the less well-defined the edge. By setting an appropriate threshold to roughly get a half-pitch linewidth, the edge roughness becomes obvious. Also, the tendency to defects is highlighted by the presence of above threshold pixels outside the edge (“bright defect pixels”), and below threshold pixels within the edges (“dark defect pixels”). More defective pixels means more information lost from the image, particularly edge position, and if severe enough, actual resist defects result.

The sum of bright and dark defect pixel % increases with decreasing pitch as expected (Figure 2).

Figure 2. Left: sum of bright defect pixel % of unexposed area and dark defect pixel % of exposed area, as a function of pitch. The effect of reducing the dose is shown for 50 nm pitch. Right: definitions of bright and dark defects.

Since the dark defect pixels dominate, a dose increase should help reduce the defect pixel %. As expected from Poisson statistics, the dose should be inversely proportional to the cube of the pitch. The # of photons absorbed scales with the thickness (proportional to pitch) and the exposed area (proportional to pitch²).

The rapid rise of required dose with decreasing pitch is a burden on EUV system throughput. Also, the resist would need to be changed to accommodate a much different (≥2X!) dose. If the throughput hit is too severe, or the resist dose is too high to accommodate, it can pose a practical resolution limit even though k1>0.25. In the case shown in Figure 3, a dose upper limit of 2x the dose used at 50 nm pitch would put 40 nm pitch as the practical resolution limit.

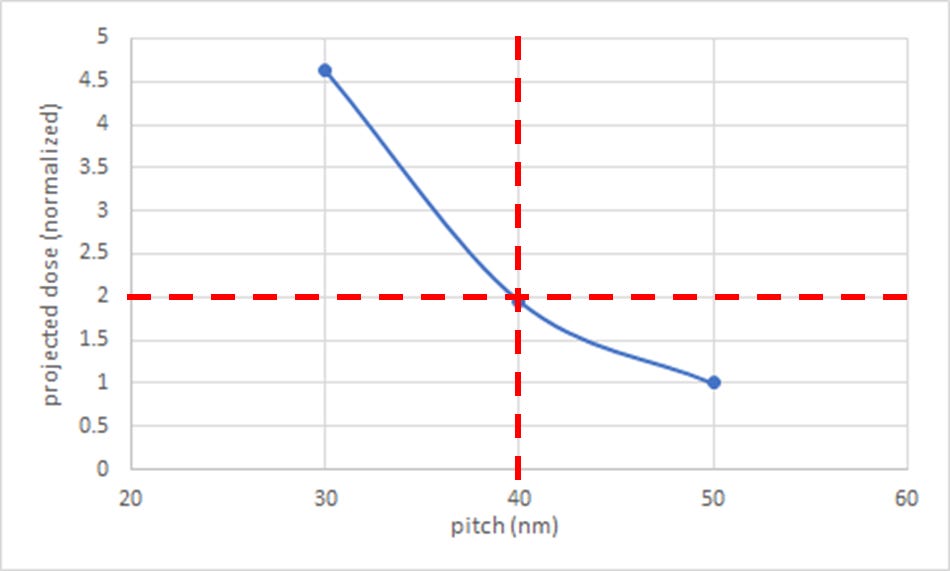
Figure 3. Projected dose varies as the inverse cube of pitch to preserve the same degree of photon noise. In this example, a dose upper limit of 2x the dose used at 50 nm pitch would put 40 nm pitch as the practical resolution limit.

To sum up, the resolution limit of EUV lithography is not determined by only the factors limiting DUV lithography. Electron blur and stochastic effects need to be considered as well. Due to stochastics, dose is expected to increase significantly as pitch decreases. With smaller pitch, fewer photons are absorbed, and there is more impact from blur. Higher dose impacts throughput, resist choice. Consequently, the practical resolution limit of EUV lithography will depend on dose as well as the resist. It is no surprise to see multipatterning is used for ~30 nm pitch and below [7].

References

[1] G. He et al., “Stochastic EUV Resist Model,” ISEDA 2023, p.477.

[2] B. J. Lin, “Optical Lithography with and without NGL for Single-Digit Nanometer Nodes,” Proc. SPIE 9426, 942602 (2015).

[3] G. Denbeaux et al., “The role of secondary electrons in EUV resist,” EUVL Workshop 2014.

[4] D. F. Ogletree, “X-rays, Electrons and Lithography: Fundamental Processes in Molecular Radiation Chemistry,” EUVL Berkeley 2017.

[5] A. V. Pret et al., ”Modeling and simulation of low-energy electron scattering in organic and inorganic EUV photoresists,” Proc. SPIE 10146, 1014609 (2017).

[6] P. Theofanis et al., “Modeling photon, electron, and chemical interactions in a model hafnium oxide nanocluster EUV photoresist,” Proc. SPIE 11323, 113230I (2020).

[7] Y-J. Mii, “Semiconductor Industry Outlook and New Technology Frontiers,” IEDM 2024 Keynote.

The full video presentation of this article is available here:

Also Read:

Stochastic Pupil Fill in EUV Lithography

Application-Specific Lithography: Patterning 5nm 5.5-Track Metal by DUV

Why NA is Not Relevant to Resolution in EUV Lithography

Share this post via:

• 
• 
• 
•