Mask and Optical Models–Evolution of Lithography Process Models, Part IV

Will Rogers said that an economist’s guess is liable to be as good as anyone’s, but with advanced-node optical lithography, I might have to disagree. Unlike the fickle economy, the distorting effects of the mask and lithographic system are ruled by physics, and so can be modeled.

In this installment, I’ll talk about two critical components of process models: mask models and optical models. Mask models come in two different flavors: those related to the 1D and 2D geometries on the mask and those related to 3D effects. Optical models are fundamental to representing the lithography imaging sequence, and have a well-established simulation methodology.

Mask Models

Historically, OPC models were calibrated based on an assumed exact match of the physical test mask and the test pattern layouts representing the test mask. However, the mask patterning process exhibits systematic proximity effects such as corner rounding and isolated-to-dense bias. In the past, it was acceptable to lump the systematic mask proximity effects into the resist process model because the mask manufacturing process is usually invariant for the life of the wafer technology. This means, however, that anytime the mask process changes substantially, the OPC model has to be recalibrated.

More significantly, the OPC model incorrectly ascribes mask behavior to the photoresist model, which limits the predictability of the model. Recent work on mask process proximity modeling is changing this (Tejnil 2008; Lin 2009; Lin 2011). This work involves calibrating a mask process model (MPC) based on mask CD or contour measurements, then referencing the MPC model to describe the mask input to the wafer OPC calibration flow. A 50% reduction in mask CD variability can be realized with this approach.

Mask models have also evolved to account for the introduction of alternating phase shift masking (PSM) into manufacturing, which raised awareness of the impact of mask topography on wafer lithography. Ultimately this aggressive PSM approach was replaced with more manufacturable solutions, including attenuated-PSM, which eliminated etched quartz in favor of a thin, partially absorbing layer.

The extensively used Kirchhoff, or flat mask approximation, assumes that the mask is sufficiently thin that the diffracted light is computed by means of scalar or vector diffraction theory. This is in contrast to rigorous electromagnetic field (EMF) simulation, which accounts explicitly for the topography and refractive indices of the mask materials, and solves Maxwell’s equations in 3D (a highly compute intensive operation not suitable for full-chip).

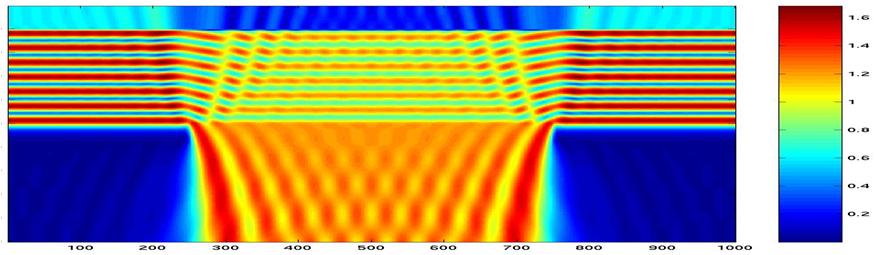
Figure showing near field intensity calculated by rigorous 3D electromagnetic field simulation.

There are many approximation methods that enable a reduction of this 3D EMF system to simpler 1D or 2D representations. Comparison to full rigorous simulation shows an advantage in accuracy by accounting for 3D mask effects versus the Kirchhoff mask, but in practice, the process model can easily adapt to effectively account for the same CD behavior. This is analogous to the mask CD effect described above. Recently, even thinner absorbing layers have been reported, which further reduce the mask 3D contribution to wafer CD variation, thus rendering the continued use of the Kirchhoff approximation a reasonable trade-off.

3D mask effects are sensitive to the angle of incidence of the light impinging upon the mask, and for high NA systems, it is necessary to account for this effect. Approximation methods are available that effectively sectorize the source then calculate the mask signal corresponding to each sector. These approaches deliver accuracy within a few nm of the rigorous simulation result.

Optical Models

Optical models represent the lithography imaging sequence. As introduced above, full chip simulations commonly employ the SOCS (sum of coherent systems) approximation to represent the intensity as a sum of convolutions of the mask m with k different optical kernels f[SUB]n[/SUB], as described in Equation 1.

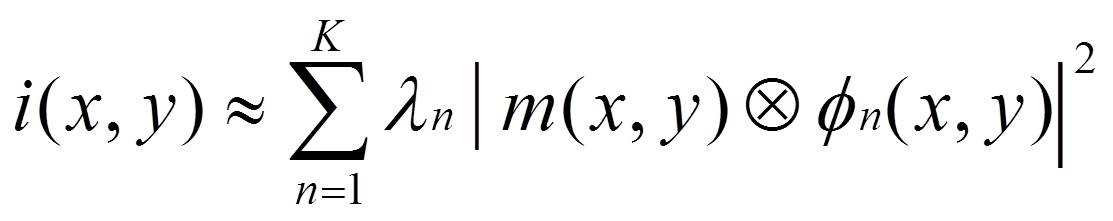
(Equation 1)

For optical models, there is a strong linear dependence of simulation time on the number of SOCS decomposition kernels used in the simulation. In addition, there is a quadratic dependence on the optical diameter associated with the model. The magnitude of the eigen value coefficients ɸ[SUB]n[/SUB] in Equation 1 decay quickly as n increases. So in practice, as a compromise between accuracy and runtime, it is often the case that 100 or fewer optical kernels are used with an OD < 2.0 μm.

There are many exposure-related factors influencing wafer CDs which can be represented in the simulation. These include wavelength, numerical aperture, ambient refractive index, film stack optical properties, exposure dose and focus, focus blur (induced by stage tilt, stage synchronization errors, or laser bandwidth), illumination intensity and polarization, pellicle thickness, and projection optics aberrations. The model parameters associated with these factors can be input as known values or can be optimized over a user-input range during calibration. Care must be taken, however, in allowing these parameters to move too far from their design values, as this may result in a less physical model. Exposure dose and focus are adjusted in the simulator to empirically match the CD behavior in terms of the scanner dose and focus. A Jones Matrix representation of the entire optical system, or alternatively individual Zernike coefficients for system aberrations can be input into the simulator directly.

It is well known that the optical proximity effect is highly dependent upon the illumination profile, and that the actual profile differs from the profile requested by the scanner recipe. Various models have been developed to describe the actual profile analytically, but it is common today to input a symmetrized version of the in-situ measured pupilgram instead of the as-designed version.

The continuous development of mask and optical models that better represent real silicon is crucial to the success (both in technology and economics) of optical lithography in upcoming process nodes. In the next installment of this series, I will discuss the semi-emperical resist and etch models used for full-chip correction and verification.

— John Sturtevant

To read the full technical paper on this topic, download Challenges for Patterning Process Models Applied to Large Scale.
Want to read past installments of this series? Part I, Part II, Part III