Concluding Inconclusives

Formal methods are a vital complement to other tools in the verification arsenal, but they’re not without challenges. One of the more daunting is the “inconclusive” result – that case where the tool seems to be telling you that it simply gave up trying to figure out if a particular assertion is true or false. Compounding the problem, these inconclusive results aren’t rare events; they can actually be quite common, especially when you’re still on the learning curve. When I was first introduced to formal I thought that this made formal at best a minor tool in verification. If proving assertions was this hit-and miss, how could it play a major role?

Turns out I was wrong, but I had to learn a bit more about formal methods to find out why. An inconclusive result doesn’t mean that all hope is lost for that assertion. As in most things, you can try harder or you can try smarter to prove the assertion. You can also change your approach to the proof. Mentor recently released a white paper illustrating some of these methods through a flow and an example. I particularly like the example so I’ll focus on that here.

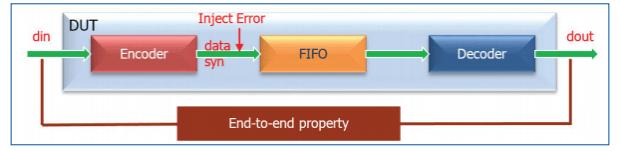
This is based on an ECC-wrapped memory, common enough, especially in safety-critical designs. The function reads a (vector) data input and forwards that together with a syndrome value to (in this case) a FIFO. The decoder pulls entries from the FIFO and outputs the data. Through this process, errors in two bits or less can be corrected. So a natural way to approach a formal proof would be to assert that the output data should always be equal to the input data, add a mechanism to inject errors on 0, 1 or 2 bits, then launch the formal prover.

If you do this, you’ll probably get lots of experience with inconclusives, thanks to the fairly complex logic in the encoder and decoder and long sequences that must be followed through the FIFO. So the first trick is to break the design into pieces; in this case, first bypass the FIFO and prove that the assertion always holds when the output of the encoder is connected directly to the input of the decoder.

How do you inject errors? The white-paper suggests a common approach with a clever wrinkle. A simple way to error a data bit is to cut that line, which you can accomplish through an external “cutpoint” command. A formal engine will assume a cut line can take any possible value and will test for all of those values, some of which will obviously differ from the (pre-cut) input values.

You want to test that the ECC will recover from errors on two or less bits, so you need to add two or less of these cuts, but it would be cumbersome to list all of the possibilities, so here comes the wrinkle. The paper suggests adding a random bus with the same width as the data bus, also undriven, so formal will consider all possible value on the bus. Then cutpoints are added to those bits on the data bus where the corresponding bit on the random bus is high. Finally, the proof is constrained to only consider cases where two or less bits on the random bus are high. In this way the formal engine does the hard work of iterating over possible combinations of errors during the course of proving.

Finally, you need to prove that the FIFO operates correctly. The good news here is that formal tools generally provide a support library (assertions and possibly constraints) to deal with common components. For example, the Mentor Questa formal tool has a predefined setup to handle FIFOs. Since you are just checking the FIFO, you can cut the data and syndrome inputs to the block, allowing the proof to consider any possible values.

You might want to do one more thing – add a couple of constraints to avoid potential false errors. If read-enable is issued when the FIFO is empty or write-enable when the FIFO is full, that could be considered out-of-spec usage, or at least beyond the bounds of this proving task. Your choice, depending on what you want to prove. Either way, you can now run a proof using the pre-packaged assertions/constraints and verify the FIFO behaves correctly under all conditions.

In summary, inconclusives are manageable, in this case by breaking the problem down into pieces and through judicious use of cutpoints, constraints and a pre-existing assertion-model for the FIFO. You just have to approach the problem in the right way. You can read the white-paper HERE.