As any semiconductor process advances to the next generation or “node”, a sticky point is how to achieve the required higher resolution. As noted in another article [1], multipatterning (the required use of repeated patterning steps for a particular feature) has been practiced already for many years, and many have looked to EUV lithography as a potential escape from more multipatterning. In reality, the requirement for multipatterning is dependent on the feature to which it is applied. This article is first in a series exploring key cases, to see when multipatterning may be avoided, and if it can’t be avoided, what is most likely the most practical way to do it. The first case to be considered will be the simplest: two features separated by a very small distance. These may represent two neighboring vias located at the ends of two separate long metal lines, for example (Figure 1).
Figure 1. Two neighboring vias at the ends of two long metal lines represent the basic case of two small features separated by a small distance.
The Rayleigh criterion
The Rayleigh criterion is a schoolbook formula giving the resolving power of an imaging system, with a given numerical aperture. The radius of the smallest spot that can be focused is given by r = 0.61 wavelength/numerical aperture. The numerical aperture here is basically the radius of the lens divided by the focusing distance (or focal length) [2]. If a second spot is located at the edge of the first spot, i.e., at this radial distance r, then it cannot be resolved. But once it is moved to a further distance, it can begin to be resolved. Hence, this distance defines a resolution limit for the minimum distance between two spot images (Figure 2).
Figure 2. The Rayleigh criterion defines the resolution between two features.
For an immersion lithography system, the wavelength is 193 nm, and the numerical aperture is 1.35, giving a minimum interspot distance of 87 nm. This distance might be reduced a little by the use of attenuated phase shifting masks; the improvement depends on the transmssion of the phase-shift mask [3]. For an EUV system, the wavelength is less narrowly defined (it is a pretty wide band), but nominally it is taken to be 13.5 nm, with a numerical aperture of 0.33, giving a minimum interspot distance of 25 nm. Unfortunately, to date, EUV lacks phase-shifting technology. A fundamental barrier is EUV’s relative lack of monochromaticity (it extends beyond the nominal 13.3-13.7 nm bandwidth), compared to the DUV excimer laser.
Getting below the Rayleigh criterion: Double patterning
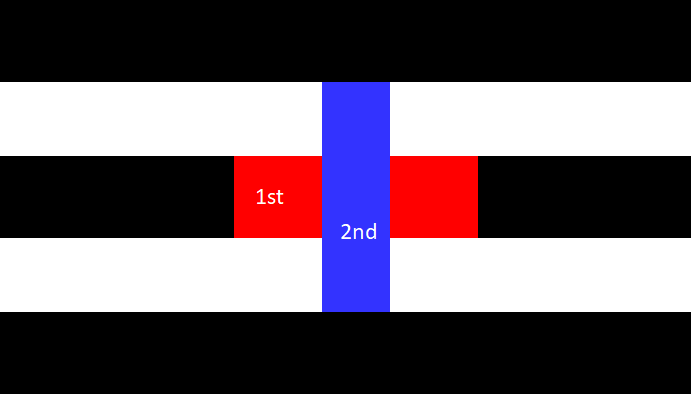
To print two features close than the Rayleigh criterion will therefore require some form of double patterning. The simplest case would be to print one of the features using one mask, then the other with a second mask (Figure 3). This approach is often referred to as LELE, an abbreviation for “Litho-Etch-Litho-Etch”. A key drawback of this approach is the obviously critical dependence on the overlay between the two exposures.
Figure 3. The LELE (litho-etch-litho-etch) approach for double patterning, applied to the two vias of Figure 1.
In an alternative form of LELE, the second exposure “cuts” the first exposed feature (Figure 4). In other words, the second exposure has opposite tone to the first. This has somewhat better alignment of the two features, at least vertically in this case.
Figure 4. In this LELE variant, the second exposure cuts the first exposed feature, being opposite in tone.
Getting below the Rayleigh criterion: Print many and trim
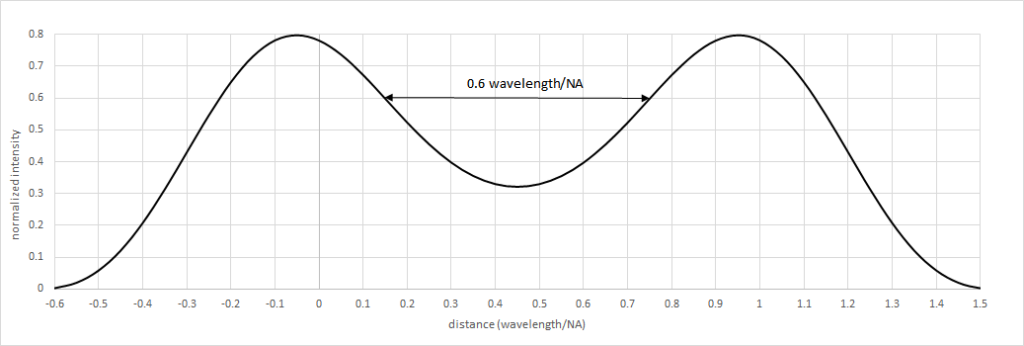
Alternatively, it is possible to print an array of the features at a tight pitch, and remove (“trim”) the ones which are not required with a second mask exposure (Figure 5), or even leave them as “dummy” features. Printing arrayed features allows the space beween features to be reduced to less than 0.6 wavelength/numerical aperture (see Appendix). The second mask exposure overlay requirement would actually be a little relaxed compared to the above LELE case, but it still has to be tighter than the distance between features.
Figure 5. The array plus trim approach, applied to the vias of Figure 1. The shaded area represents a blocking mask to prevent the previously printed array features from being further etched.
No EUV advantage for sub-25 nm isolated pairs?
A careful consideration of the above techniques may make it clear that patterning isolated (or else sufficiently widely separated) pairs of features spaced by less than 25 nm can be done by two immersion exposures (LELE style), one EUV exposure plus one immersion exposure (array plus trim), or two EUV exposures (LELE or array plus trim). The immersion-only LELE approach is more sensitive to overlay than an array plus trim approach using EUV, but with current capabilities of ~2 nm already established with immersion tools [4], for distances of ~15-20 nm, there is no real advantage in going to EUV for this case.
Appendix: Rayleigh criterion (k1=0.61) vs. k1<0.61
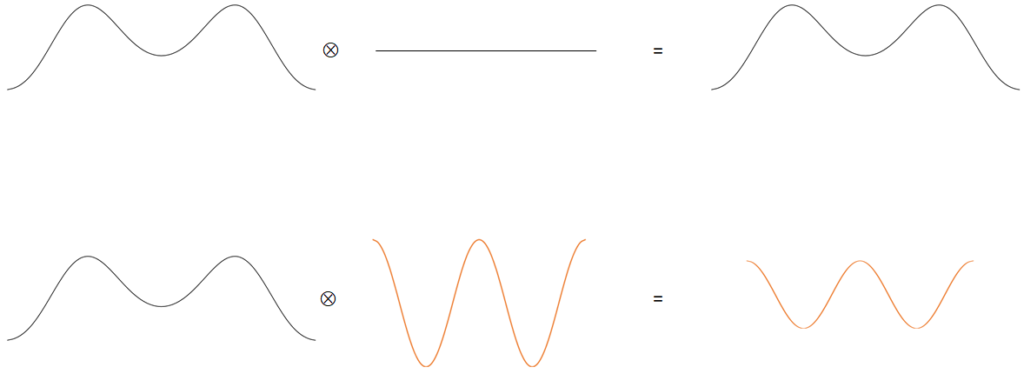
Some of you may have the reasonable question, how does the Rayleigh criterion above not conflict with the low k1 (distance = k1 * wavelength/numerical aperture, k1<0.61) cases commonly encountered in immersion lithography? This will be covered more explicitly in the next article, but for now the question can be answered with reference to Figure 6. Basically, the Rayleigh criterion addresses the smallest image of a point, i.e., the point spread function. For an assembly of features, the point spread function is mathematically convolved with the locations of the features. When the features are spread widely, the width of the point spread function obviously dominates the image. However, when the features are densely packed together, at distances comparable to the Rayleigh criterion or even less, the width of the point spread function no longer impacts the image, but instead the spatial frequency corresponding to the pitch of the features determines the image. The point spread function only contributes to the blur (contrast degradation) of the image.
Figure 6. When the point spread function is convolved with a wide pitch (top) it dominates the image. When it is convolved with a dense pitch of comparable dimensions (bottom), the pitch dominates the image.
More quantitatively, we can examine the image produced by the (coherent) illumination of two points in the object plane. This is shown in Figure 7.
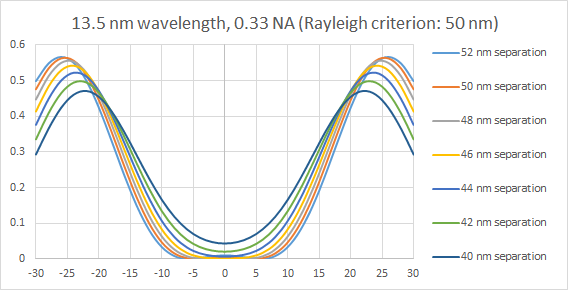
Figure 7. Two points separated by a given distance in the object plane appear wider in the image plane, when the object separation is at the Rayleigh criterion or less.
When the two objects are separated by the Rayleigh criterion or less, the image shows a wider than actual separation. Furthermore, the peak intensities are reduced and the central region shows higher intensity throughout. It is due to the growing influence of the neighboring point’s diffracted field in the image plane.
References
[1] https://www.linkedin.com/pulse/how-semiconductor-industry-got-itself-multipatterning-frederick-chen/
[2] B. E. A. Saleh and M. C. Teich, Fundamentals of Photonics (John Wiley & Sons, 1991), p.131.
[3] R. Socha et al., “Resolution Enhancement with High Transmission Attenuating Phase Shift Masks,” Proc. SPIE 3748, 290 (1999).
Share this post via:








Flynn Was Right: How a 2003 Warning Foretold Today’s Architectural Pivot