A DVCon Tutorial on Advanced Formal Usage

Synopsys has been quite active lately in their messaging around formal verification. One such event at DVCon this year was a tutorial on some of the more advanced techniques/ methodologies that are accessible to formal teams, mostly presented by customers, though opened by a Synopsys presentation. The tutorial covered so many bases that I won’t try your patience by reviewing it all in one blog. Here I talk about the Synopsys and Samsung talks; there will be a follow-on blog covering the NVIDIA and Qualcomm presentations.

Iain Singleton was a hardware engineer at Imagination Tech before he moved into formal verification support at Synopsys and posted at least a couple of papers (with Ashish Darbari and others) on formal methods while at IMG. His topic for this talk was use of invariants and inductions to improve convergence in formal proving. I was confused at first about these methods, but I’ve got (I think) a clearer picture now.

The point of invariants is to reduce the size of the proof state-space to encourage convergence. Invariants are related to assume-guarantee methods where you split a big problem into two parts, say A and B, assume certain properties must hold on inputs to A in your first sub-proof, then prove/guarantee the properties you assumed in your second sub-proof. Invariants are like those intermediate properties except no design-split is required; you plant them in the design. In the example above, Iain starts with a complex assertion he breaks it down into sub-assertions and continues breaking down until he is able to prove relatively simple assertions. Turn those into constraints and the state-space shrinks! Then prove the next more complex invariant candidates and so on up to the main property you want to prove.

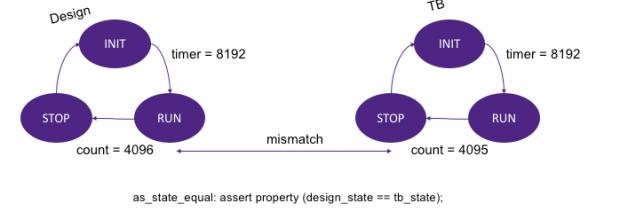
Induction is a little trickier to grasp but very useful. The idea is that if you can prove a property is true in one case, and you can prove if it is true at some cycle it must also be true at the next cycle, then it must always be true. Iain demonstrated this through a proof on a small FSM with significant sequential depth (always challenging for formal). If you start in the reset state with the assertion above, it will either take forever to find the bug or more likely the tool will give up. Instead Iain replace the assertion with this:

as_ind_state_equal: assert property (design_state == tb_state |=> design_state == tb_state);

See the difference? Instead of jumping straight to trying to prove the design state and TB state are always equal, instead you go for a proof that if they are equal in some cycle, then they must also be equal in the next cycle. One more thing – you don’t start in the reset state; you start in an unconstrained state and rely on the magic of the formal engines to find a counter-example (CEX) quickly. Which they do in 2 cycles in this example!

Finally, you can combine induction and invariants into something truly powerful – inductive invariants. From a non-reset state, find a CEX to a property you would like to use as a constraint. Then use an inductive approach to prove this CEX is not possible. Then use your constraint as an invariant in larger proofs, again with the goal of greatly reducing state-space for your primary objective. Pretty clever stuff but well within the grasp of sharp engineers.

Shaun Feng from Samsung Austin R&D provided a view of efficient formal modeling techniques. He should know; he has led formal verification over 10 years at Samsung, Oracle Labs and NVIDIA. Shaun opened with the basics: how to efficiently get to useful proofs as quickly as possible. So cut-points, black-boxes, assume-guarantee, abstracting design by shrinking size, grouping assertions by similar cones of influence and using proven assertions as invariants to cut down the state space (see above). One interesting idea for me was symbolic constants. These are values you want to remain stable (after reset) through the proof but at an unknown/random value. Shaun showed an example where this could be useful in proving properties for two types of arbiter (round-robin and priority) and for an in-order transport proof (for a bus protocol check).

Think about a priority arbiter. This has some equal number of req and grant signals. One requirement is that if there is a request on req(n) and a request on req(m) and m is less than n, there cannot be a grant on n before there has been a grant on m. You could enumerate and test all the possibilities but that would be painful. Instead, you use symbolic constants for m and n; they’re randomized coming out of reset but also stable through the proof, so you get to cover all possibilities in one proof. Shaun elaborated similarly on the round-robin and in-order transport examples which are worth studying for the methods he describes.

Sean had some interesting comments on formal and simulation. First, he noted that symbolic constants obviously don’t map directly into simulation, so you have to use a little conditional compile code to enable the symbolic constant in formal runs and a random value in simulation runs. Why does he bother, instead just going with the formal proof? Shaun echoed something I have heard elsewhere – that even though he has proven his assertions in formal, he still runs them in simulation signoff.

A member of the audience asked if Shaun had ever missed a bug in formal. He implied this was rare, but he had once missed a clock-gating bug. Naturally this could be attributed to incomplete assertion coverage (though he added that RTL design had changed after formal signoff was wrapped up) but how do you prove you don’t have that problem? There are coverage techniques leading us towards better confidence, but Shaun admitted because of that bug, he’s still not comfortable with formal-only signoff and will continue to use simulation with proven assertions to handoff.

You can learn more about the Synopsys VC Formal solution HERE.