Making Full Memory IP Robust During Design

Looking at a typical SoC design today it’s likely to contain a massive amount of memory IP, like: RAM, ROM, register files. Keeping memory close to the CPU makes sense for the lowest latency and highest performance metrics, but what about process variations affecting the memory operation? At the recent DAC conference held online I was able to get some answers by attending a Designer Track session entitled, “Ensuring Design Robustness on Full Memory IP using Sigma Amplification“, presented by Ashish Kumar, ST Microelectronics.

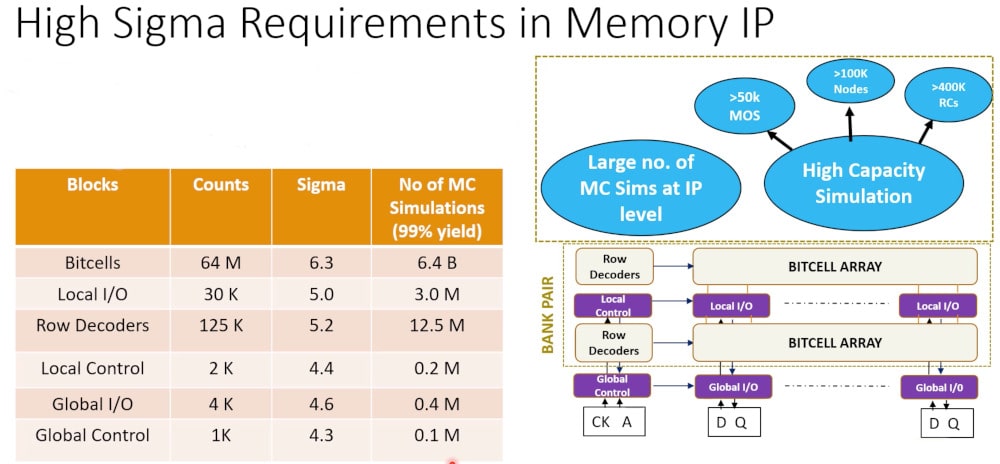
Ashish showed that for a 64Mb SRAM there are over 50,000 MOS devices, 100K nodes and 400K extracted RC parasitic elements, and such a large netlist requires a large number of Monte Carlo simulation runs to ensure robustness. The blocks comprising this SRAM include Bitcells, Local I/O, row decoders, local control, global I/O and global control, as shown below:

There are 64M bit cells and they require a 6.3 sigma analysis, and with classical Monte Carlo it requires 6.4B simulations to achieve a 99% yield, something that cannot be accomplished in a reasonable run time, so clearly we are in trouble to achieving a robust design. The other blocks inside of the memory have lower counts and corresponding lower sigma goals.

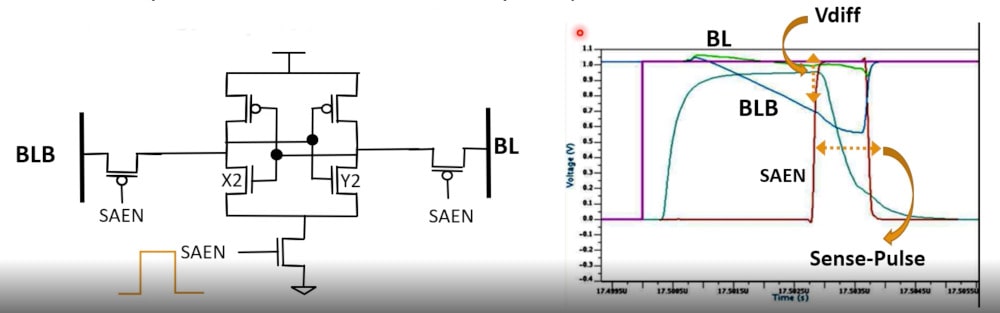
The actual bit cell schematic uses seven MOS transistors, and for a read operation the signal SAEN pulses high, then the Bit Line (BL) and Bit Line Bar (BLB) nodes start to diverge in value creating Vdiff. The larger the value of Vdiff the more stable and robust our memory cell design is.

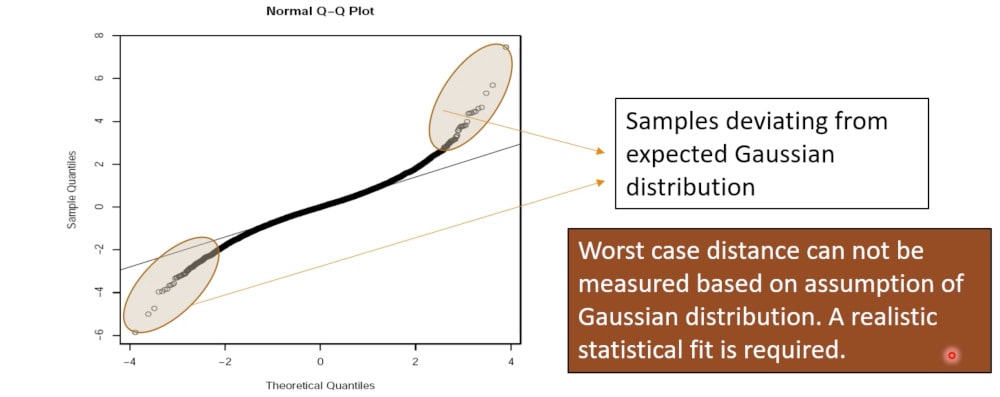
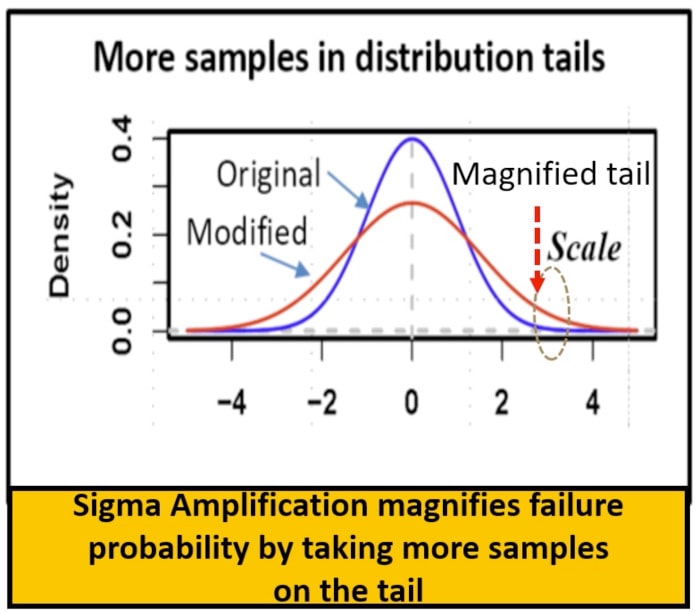
Using a traditional SPICE circuit simulator like HSPICE from Synopsys you could get 100 Monte Carlo runs in a reasonable amount of time, or with the high-capacity CustomSim tool maybe 1,000 runs, but both of those fall short of the 6.4B runs required get our robust design goals met. Process variations are no longer occurring with Gaussian distributions, see the plot below for the areas circled in Brown color, so to get a robust design we need a method to statistically fit these distributions.

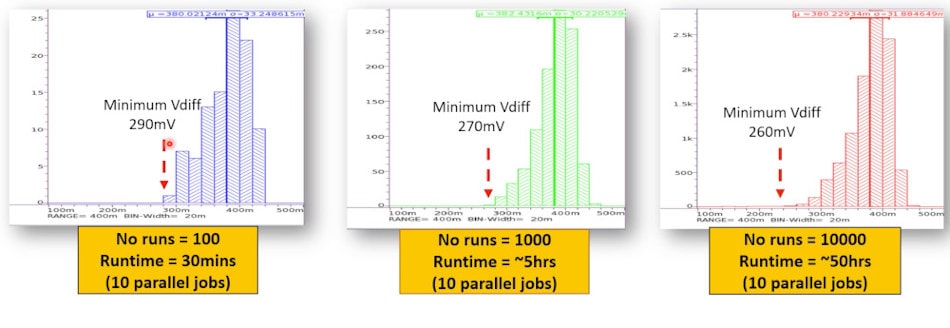
The value of Vdiff can be measured while running Monte Carlo simulations with a varying number of runs, and we find that with more runs the lower the value of Vdiff becomes. For 10,000 runs we find that the value of Vdiff falls to 260mV, but that it takes about 50 hours for circuit simulation to complete.

A normal Gaussian distribution is shown in Blue, but we really want to look at the tail of the distribution so if a statistical sample is taken in the tail region as shown by the Red curve then fewer simulations are required. This technique is called Sigma Amplification.

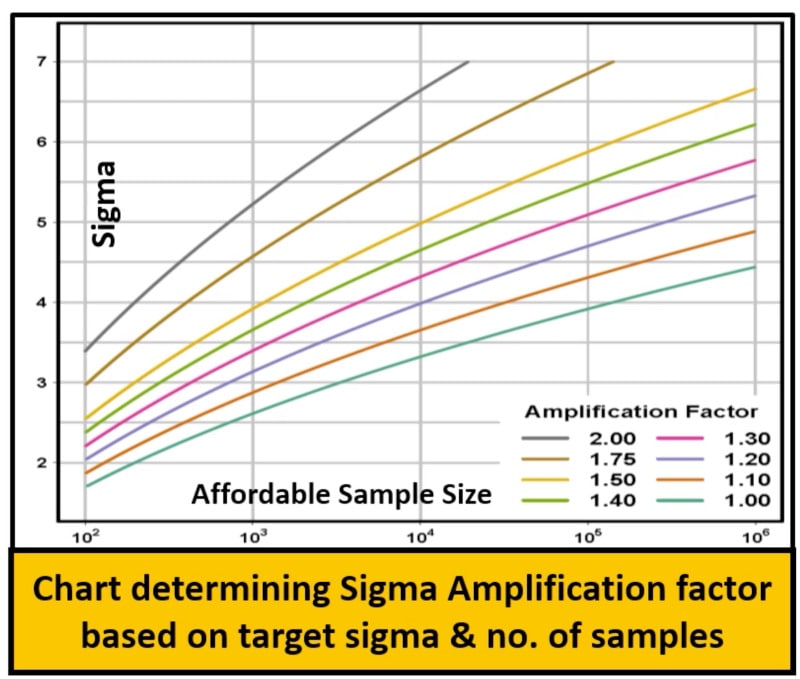
Within the Synopsys circuit simulators you can choose a Sigma Amplification value, and they recommend a value of 2 or smaller (shown in Grey) in order to reach an affordable sample size.

 

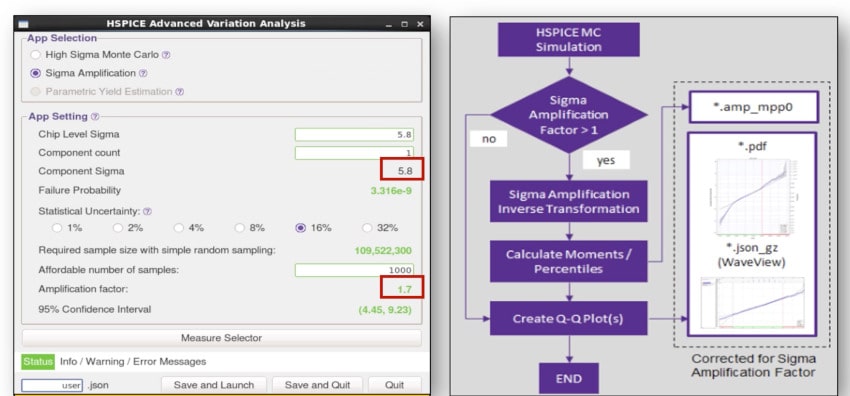
In the HSPICE GUI a designer can reach 5.8 Sigma for a memory block, but instead of taking 109,522,300 Monte Carlo runs it only takes 1,000 runs by using a Sigma Amplification of 1.7:

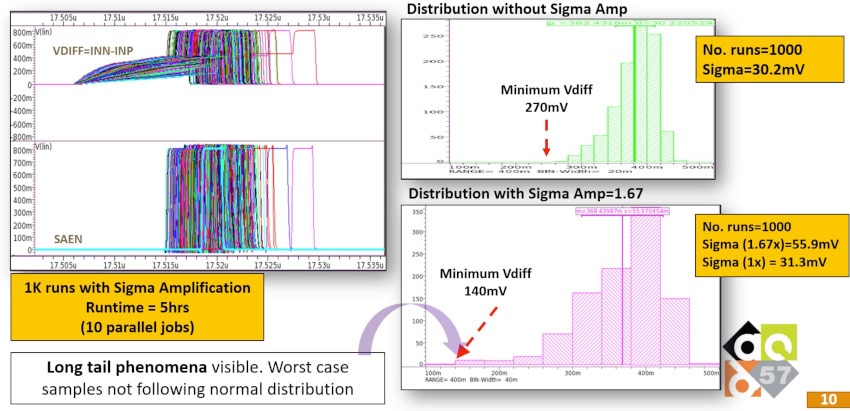
The minimum value of Vdiff using traditional Monte Carlo with 1,000 runs is 270mV, while Vdiff is calculated to be 140mV when using a Sigma Amplification value of 1.67, which proves that we are finding even more worst case samples that are not following a normal distribution. In just 5 hours we know that Vdiff has a much lower value than before using Sigma Amplification, something that was not possible with traditional Monte Carlo simulations.

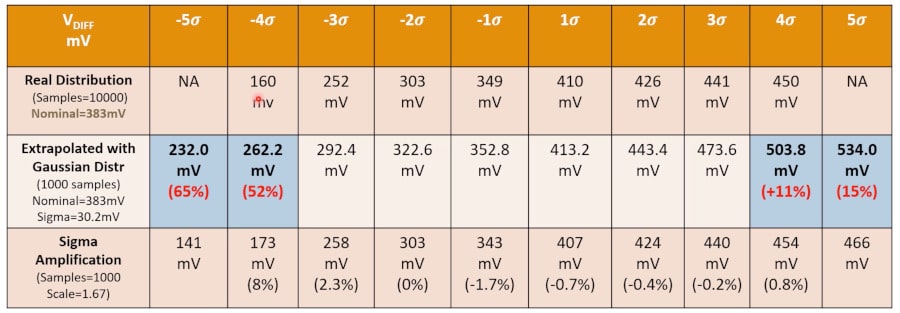
Comparing Vdiff versus distributions, consider three approaches:

• Real distribution – traditional Monte Carlo with Gaussian distribution
• Extrapolated with Gaussian distribution
• Sigma Amplification

Using real distribution with 10,000 samples we can only achieve +/- 4 sigma results. If we  extrapolate with gaussian distribution, then Vdiff can reach +/- 5 sigma in 1,000 samples, but our  Vdiff values become inaccurate, so faster incorrect answers. With the Sigma Amplification approach we can reach +/- 5 sigma results, using only 1,000 samples while maintaining acceptable accuracy levels.

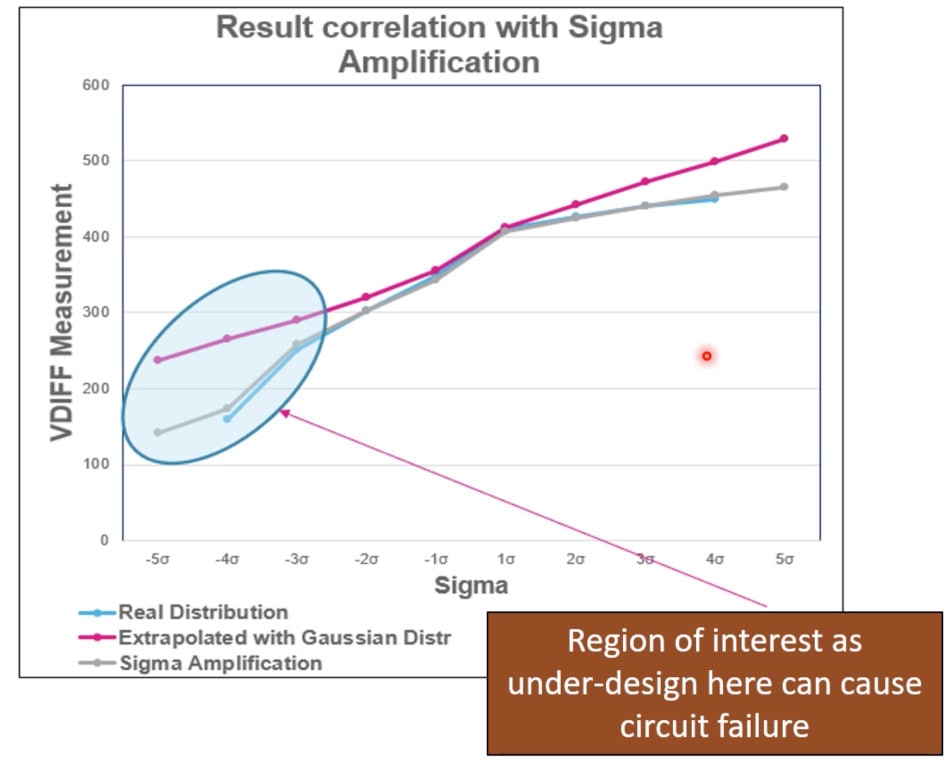
Another way to visualize these three approaches is to plot Vdiff as a function of Sigma. The Real Distribution is shown in Blue color, and the most accurate comparison is Sigma Amplification in Grey, while the least accurate approach is Extrapolated with Gaussian distribution in Purple.

 

Summary

Memory IP design is important for modern SoCs, so getting robust IP blocks is quite important to reliable operation over the product lifetime, but using traditional Monte Carlo approaches with Gaussian distributions during the design phase just takes too much time. Fortunately for us, there are approaches to focus on the tail regions to uncover the worst-case conditions by using a statistical distribution approach. Synopsys calls their approach Sigma Amplification and the theory is borne out on real memory IP, so designers can now achieve a much higher sigma goal with fewer Monte Carlo runs.

Also Read:

ARC Processor Virtual Summit!

Synopsys Webinar: A Comprehensive Overview of High-Speed Data Center Communications

Accelerating High-Performance Computing SoC Designs with Synopsys IP

Share this post via:

• 
• 
• 
•