Finite state machines (FSMs) are a very convenient way of describing certain kinds of behavior. But like any other aspect of design, it is important to get everything right. Since finite state machines have been formally studied, there is a lot of knowledge about the types of bugs that a finite state machine might exhibit.
When flipflops were considered extremely expensive, a lot of work was done on optimizing the state encoding to use the minimum number of flops. Unfortunately this tended to mean using the maximum number of gates around the state register, since essentially the state had to be decoded and then the new state re-encoded. Today, many finite state machines are implemented using one-hot encoding, meaning that each state has its own flop and all others should be zero, which is simple to understand and implement and has well-behaved timing. Another common encoding is gray-encoding in which every transition changes just a single bit in the state register, and as a result can have good low power attributes although finding a suitable encoding is not always easy (or even possible).
Although a finite state machine can have a large number of states, this is something best avoided since it makes them hard to create, hard to understand and wasteful of area and power. Almost always it is better to decompose a large finite state machine into multiple communicating smaller ones.
The most common errors in finite state machines are deadlock and unreachable states. A deadlock state is one that once reached, no combination of inputs will cause the state to be exited. An unreachable state is one that can never be entered. Another more subtle problem is handling asynchronous inputs, inputs from a different clock domain from the state machine register clock. This requires some form of synchronizer like other clock domain crossing bugs.
Obvious measures of the complexity of an FSM are the number of states and the number of transitions. A more subtle measure is the depth of the FSM, the maximum number of transitions that are possible from the initial state without re-entering any state. The depth should be kept small if possible to simplify verification.
Generally, an FSM has a single initial state which it enters when the system is powered up or reset (or the FSM itself is reset). If an FSM cannot be reset, then it comes up in an unknown state and this will make verification unnecessarily complex.
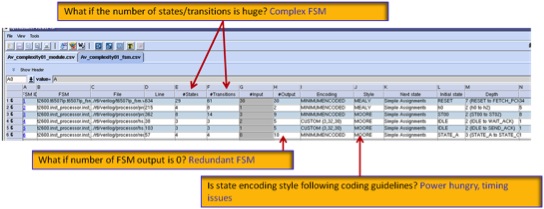
Manually validating the correctness of all but the smallest FSM is complex. Atrenta has developed an extension to its SpyGlass product family to address these FSM design and verification issues. SpyGlass Advanced Lint automatically recognizes FSMs, reports their metrics and checks for deadlock and unreachable states.
For more information read the white paper on Techniques for FSM Design and Verification.
Real men have fabs!