Mathematics are Hard – That is Why AI Needs Mathematics Hardware

The field of artificial intelligence has relied on heavy inspiration from the world of natural intelligence, such as the human mind, to build working systems that can learn and act on new information based on that learning. In natural networks, neurons do the work, deciding when to fire based on huge numbers of inputs. The relationship between the inputs, in the form of incoming synapses, and the act of firing an outgoing synapse is called the transfer function. In the wetware of our brains there is a complex interplay of neurotransmitters and ion flux across cell membranes that define the activation function for a given neuron. In some cases, thousands of incoming inputs can control firing. In each part of the brain where information is processed there might be a multitude of parallel neurons layered in series to perform a task.

So too, in artificial neural networks, there are layers of highly interconnected neurons that receive input and must decide to fire based on an activation function. Over the years, AI researchers have experimented with a wide range of activation functions, i.e. step function, linear, sigmoid, etc. Sigmoid and sigmoid-like functions have become popular because of their responsiveness and suitability for building multilayered networks. There are, of course, other desirable types, but many of these share the need to vary sensitivity as a function of input level.

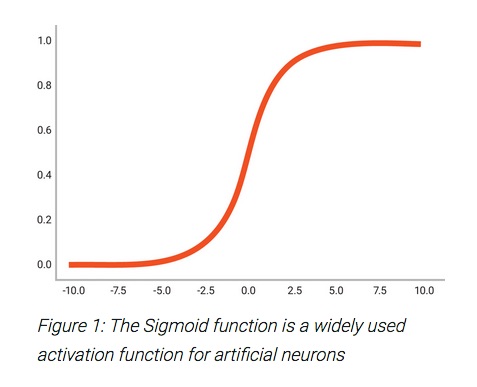
A direct consequence of the use of sigmoid functions, with their varying sensitivity, is the use of floating point operations to implement the activation functions for many classes of neural networks. Initially it was sufficient to rely on the processing capabilities of standard processors for the implementation of neural networks, but with increasing requirements for throughput and optimization, specialized hardware is used more and more often. Specialized floating point processing has proven itself to offer big benefits. In addition to lack of parallelization, CPU based floating point units often did not fit the precision, area, power or performance needs of neural networks. This is especially true for neural networks tailored for specific tasks.

It makes more sense for designers of SOCs that perform neural network processing to pick and choose the best floating point IP for their application. The considerations might include optimization through fusing specific functions, controlling rounding, and minimizing redundant normalization operations. It is also worth pointing out that when lower precision will work, reductions in area and power can be made.

It was with great interest that I read an article by Synopsys on how their DesignWare library offers floating point functions that can be used for neural network implementations. When their floating point operations are pipelined it is possible to use their Flexible Floating Point (FFP) format to transfer intermediate results and meta data between operations. This gives designers the ability to precisely specify all aspects of the float operations. To ensure ideal performance and behavior, Synopsys supplies bit-accurate C++ libraries, allowing system simulation that includes desired floating point operations.

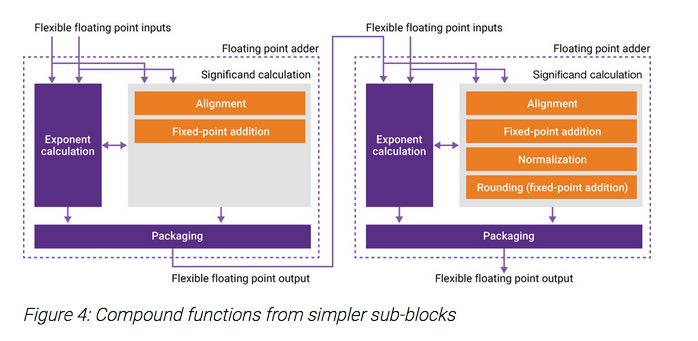
In some ways, the future of neural networks is about lower precision. A lot of work is going on into driving towards sparse matrix operations at the lowest resolutions. However, at these precisions the sensitivity and accuracy of the operations must be ensured. Designers need the ability to explore and then define the optimal configurations and operation of special purpose neural networks. The Synopsys DesignWare IP offerings for floating point functions seem like a useful tool to accomplish this. The article referenced above can be found on their website.