Breaking the Sorting Barrier for Directed Single-Source Shortest Paths

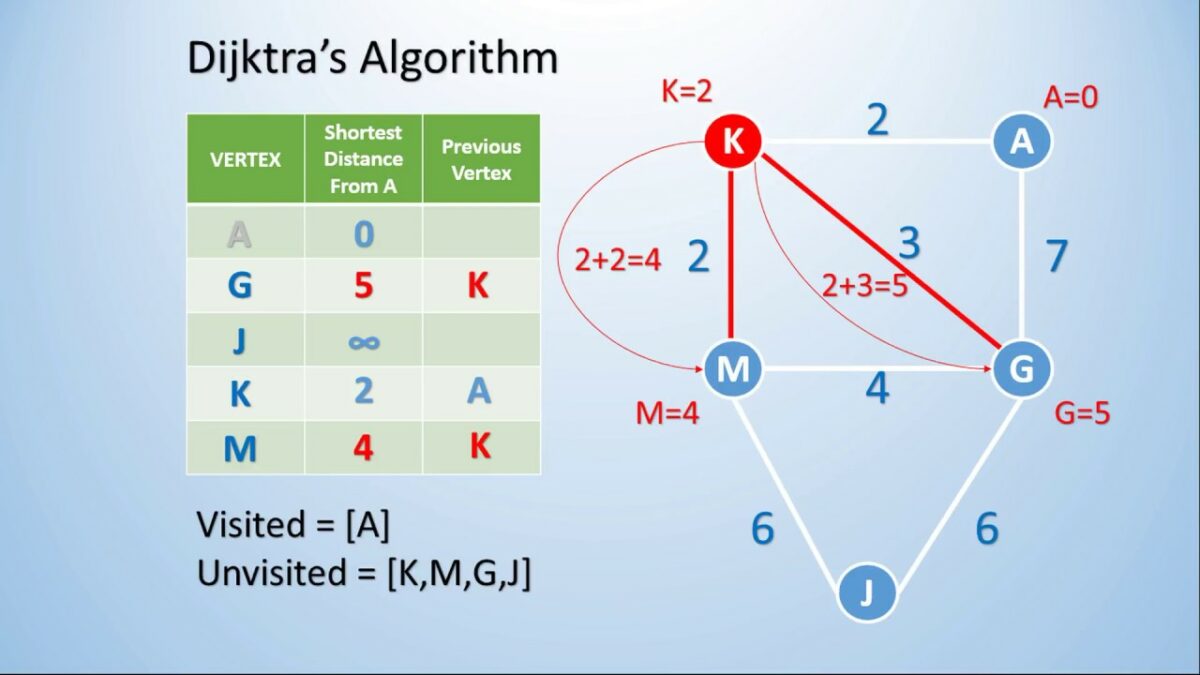
Problem & significance.
Single-source shortest paths (SSSP) on directed graphs with non-negative real weights is a pillar of graph algorithms. For decades, the textbook gold standard has been Dijkstra’s algorithm with good heaps, running in the comparison-addition model (only comparisons and additions on weights). Because Dijkstra effectively maintains a total order of tentative distances, many believed its  “sorting cost” was an inherent barrier on sparse graphs. The new paper “Breaking the Sorting Barrier for Directed Single-Source Shortest Paths” overturns that belief with a deterministic algorithm for directed graphs—strictly on sparse inputs and the first to beat Dijkstra’s bound in this model.

Model & setup.
The result holds in the comparison-addition model with real, non-negative edge weights. The authors adopt standard simplifications that preserve shortest paths: (i) make the graph constant-degree via a classical vertex-expansion gadget ensure uniqueness of path lengths by a lexicographic tie-breaking scheme that can be implemented with some overhead. These choices streamline the analysis without changing correctness.

Core idea in one line.
Blend the ordering discipline of Dijkstra with the bulk-relaxation power of Bellman–Ford, but never fully sort the frontier. Instead, shrink the frontier so only a fraction of “pivots” need attention at each scale, thereby skirting the sorting bottleneck.

From barrier to breakthrough: two levers.

1. Frontier reduction via “pivots.”
   At any moment, Dijkstra’s priority queue reflects a frontier $S$ of vertices whose outgoing edges can unlock progress. If one naively kept selecting the minimum, sorting resurfaces. The paper instead introduces a FindPivots subroutine that runs $k$ rounds of bounded relaxations (Bellman–Ford style) and classifies vertices according to whether their shortest path crosses at most $k$ frontier-interval vertices. Those that finish become complete. The others are “covered” by root vertices whose shortest-path subtrees are large. Only these roots—the pivots—must persist.

2. Recursive bounded multi-source SSSP (BMSSP).
   Rather than run one monolithic Dijkstra, the algorithm performs a divide-and-conquer over distance scales.

A partial-sorting data structure.
To orchestrate sources across recursive calls without full sorting, the authors design a block-based structure supporting: Insert, BatchPrepend (efficiently add a batch of strictly smaller keys), and Pull (extract up to $M$ smallest keys plus a separating threshold). This lets the algorithm “sip” from the smallest distance ranges as needed, while updates from relaxations are appended efficiently, avoiding global reordering.

Context & novelty.
Earlier, it was shown that Dijkstra is optimal if one insists on outputting the full ordering of vertices by distance. This paper sidesteps that constraint: it outputs distances without maintaining a total order, breaking the “sorting barrier.” It also delivers the first deterministic improvement even relative to prior randomized gains on undirected graphs, strengthening the case that the barrier is not fundamental.

Takeaways:

Theory: A clean, deterministic path past $n\log n$ for directed SSSP in a realistic algebraic model.

• Technique: A reusable template—bounded multi-source recursion, pivot selection, and partial sorting—that may inform faster routines for other path problems under comparison constraints.

• Outlook: Extending these ideas to richer weight domains or dynamic settings could unlock further speedups where sorting once seemed inevitable.

The full paper:  Breaking the Sorting Barrier for Directed Single-Source Shortest Paths